Historia liczb naturalnych sięga bardzo głęboko wstecz. Śmiało można stwierdzić, że te najprostsze operacje liczbowe towarzyszyły człowiekowi od zarania dziejów, ale rozwój ludzkości to rzecz jasna również rozwój umiejętności liczenia. Obecnie nie jest możliwym wyobrażenie sobie świata bez zastosowania liczb.
Liczby pierwsze – co o nich wiemy?
Liczby pierwsze to liczby naturalne mające dokładnie dwa dzielniki: 1 i samą siebie. Zbiór liczb pierwszych oznaczany jest najczęściej przez ℙ. Liczb pierwszych istnieje nieskończenie wiele, a najmniejszą i jedyną parzystą z nich jest 2. Wydawać by się mogło, że miano najmniejszej liczby pierwszej przypada liczbie 1, jednak ma ona tylko jeden dzielnik, dlatego nie należy do tego zbioru. Dowolną liczbę złożoną można przedstawić jako iloczyn liczb pierwszych, co nazywamy rozkładem na czynniki pierwsze.
Już od starożytności wielu matematyków trudzi się poszukiwaniem wzorca na uporządkowanie zbioru liczb i wyznaczenie liczby jak największej. Obecnie największą znaną liczbą pierwszą wyznaczoną według wzoru Mersenne’a postaci 2n–1, gdzie n jest liczbą naturalną, jest liczba 282589933–1 mająca 24 862 048 cyfr. Za wyznaczenie liczby pierwszej mającej 100 mln cyfr Electronic Frontier Foundation wyznaczyła nagrodę 150 tys. dolarów, za liczbę pierwszą mającą minimum miliard cyfr – 250 tys. dolarów, a za każdą liczbę pierwszą poniżej 100mln znaków – 3 tys. dolarów.
Algorytmy wyznaczania
Istnieje wiele algorytmów wyznaczania liczb pierwszych. Jednym z najstarszych i ciągle najpopularniejszym jest Sito Eratostenesa. Autorstwo przypisuje się Eratostenesowi z Cyreny, greckiemu matematykowi żyjącemu w latach 276-194 p.n.e. Jego ideą jest wykreślanie z listy potencjalnych liczb pierwszych tych wartości, które na pewno nie są pierwsze. W praktyce wygląda to następująco:
Ze zbioru liczb naturalnych z przedziału [2, n] należy wybrać najmniejszą liczbę pierwszą – będzie to liczba 2 – i wykreślić wszystkie jej wielokrotności większe od niej samej. Dla zobrazowania tych działań, weźmy na przykład przedział [2, 100].
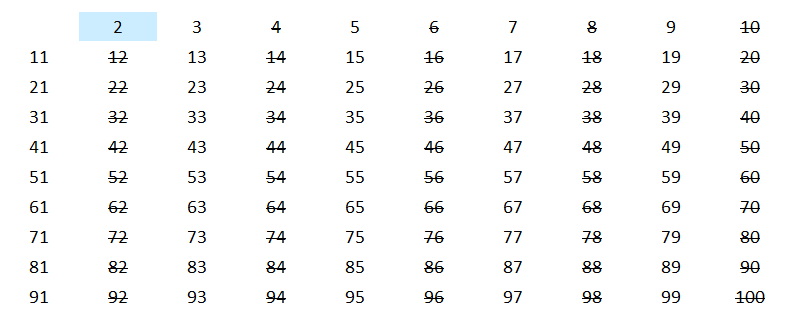
Następnie z pozostałych liczb należy wybrać najmniejszą niewykreśloną liczbę – będzie to liczba 3 – i również wykreślić wszystkie jej wielokrotności większe od niej samej.
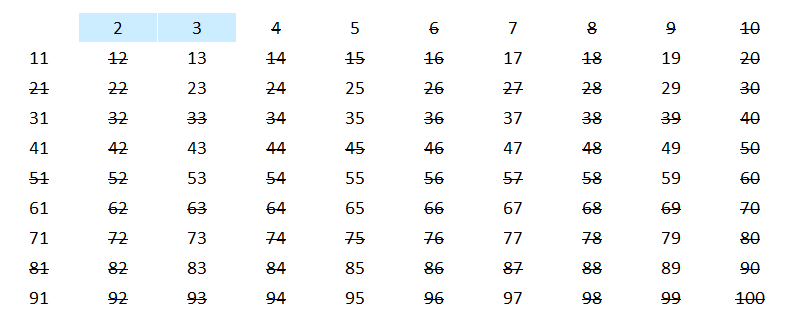
Wykreślanie należy powtarzać do momentu, gdy liczba i, której wielokrotność jest wykreślana, będzie większa niż pierwiastek z liczby n.
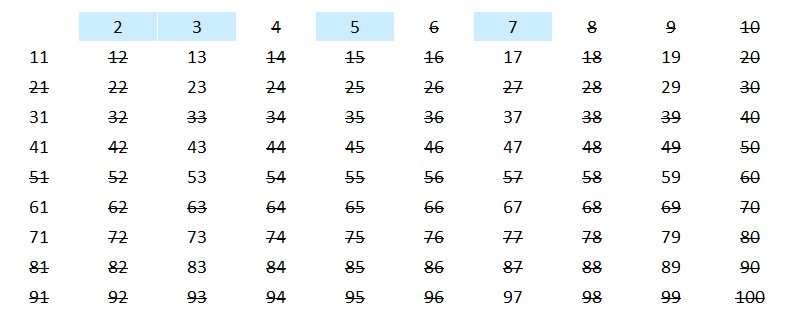
W ten sposób dochodzimy do momentu, w którym wszystkie niewykreślone liczby z przedziału [2, n] są liczbami pierwszymi.

Liczby pierwsze – szczególne rodzaje
Wyróżnić można wiele grup liczb pierwszych charakteryzujących się szczególnymi właściwościami. Oto kilka z nich wraz z przykładami:
- bliźniacze – to takie dwie liczby pierwsze, których różnica wynosi 2
- 5 z 3 oraz z 7
- 71 i 73
- 4421 i 4423
- czworacze – liczby pierwsze postaci p, p+2, p+6, p+8, czyli pary liczb bliźniaczych w najbliższym możliwym sąsiedztwie
- 5, 7, 11, 13
- 101, 103, 107, 109
- 72221, 72223, 72227, 72229
- lustrzane – pary liczb pierwszych, z których jedna powstaje przez zapisanie cyfr drugiej w odwrotnej kolejności
- 79 i 97
- 113 i 311
- 1217 i 7121
- palindromiczne – liczby pierwsze, które czytane od przodu do tyłu jak i od tyłu do przodu są tymi samymi liczbami
- 373
- 19991
- 123424321
Zastosowanie liczb pierwszych
Obecnie liczby pierwsze i własności ich dzielników są powszechnie wykorzystywane nie tylko w matematyce. Przykładem mogą być algorytmy szyfrowania służące do ochrony danych w systemach komputerowych, kart bankowych, ochrony prywatności komunikacji internetowej i telefonicznej.
